Mastering Mixed Fractions: A Complete Guide


Intro
Mixed fractions have a reputation for being a tricky concept when it comes to mathematics, yet they play a significant role in everyday calculations. Understanding the structure of mixed fractions not only enhances mathematical skills but also fosters problem-solving abilities that students carry into various aspects of life. This guide aims to clarify mixed fractions, explaining how to simplify them and their applications in real-world situations. By the end of this discussion, educators and parents alike will be equipped with detailed knowledge and practical tips to facilitate learning.
Interactive Learning Games
In today’s digital age, learning can often feel tedious, especially when it involves numbers and fractions. Enter interactive learning games — an engaging way to grasp the complexities of mixed fractions while having fun at the same time. Below, we dive into some popular games that not only entertain but also educate young minds.
Popular Games
- Fraction Frenzy
- Pizza Fraction
- Fraction Munchers
Description of top educational games
Fraction Frenzy is a colorful, fast-paced game that helps students grasp the concept of mixed fractions through timed challenges. Players must quickly convert mixed fractions into improper fractions, racing against the clock. This adds a thrilling twist to learning that keeps kids on their toes.
Pizza Fraction combines a classic favorite with mathematics, where children can create their own pizzas using mixed fractions. This game visually demonstrates how fractions work together, making it easier for learners to understand.
Fraction Munchers uses a cute monster theme, where children 'feed' monsters the correct fraction answers. This interactive element adds an enjoyable layer to learning, motivating students to practice more.
Benefits of playing educational games for kids' cognitive development
Educational games offer numerous benefits for cognitive development, including:
- Enhanced Problem Solving Skills: Students learn how to tackle challenges through gameplay.
- Critical Thinking: As players decide the best strategies, their ability to think critically improves.
- Retention of Knowledge: Fun activities often lead to better memory retention compared to traditional rote learning.
"Learning through play is not a new concept, but its effectiveness in grasping difficult topics like mixed fractions cannot be overstated."
Game Reviews
When it comes to understanding mixed fractions, not all games are created equal. Here’s a quick overview of the strengths and weaknesses of our featured selections.
- Fraction Frenzy
- Pizza Fraction
- Fraction Munchers
- Strengths: Fast-paced and highly engaging. Each level presents new challenges.
- Weaknesses: Can become repetitive over time.
- Strengths: Offers visual representation of fractions, making concepts easier to grasp.
- Weaknesses: Limited levels may reduce engagement over time.
- Strengths: Cute and funny monsters keep students engaged.
- Weaknesses: The interface may be a little confusing for young learners.
Comparison of gameplay and learning outcomes
When comparing these games, Fraction Frenzy provides a high degree of challenge that is suitable for slightly older students who have a grasp on the basics. On the other hand, Pizza Fraction may be ideal for younger children due to its relatable context and ease of understanding. Fraction Munchers serves as a bridge, blending fun and education, making it effective for learners across the board.
Educational Topics
Understanding mixed fractions is just one piece of the educational puzzle. To provide a well-rounded learning experience, it's beneficial to explore various topics that intertwine with mathematics. The following subjects complement the understanding of mixed numbers and fractions:
- Math: Enhances critical thinking and analytical skills.
- Science: Encourages inquiry-based learning.
- Languages: Improves literacy alongside numerical comprehension.
Importance of interdisciplinary learning for holistic development
Interdisciplinary learning encourages students to connect different subjects, helping them see the relevance of mathematics in daily life. For example, when exploring percentages in science, understanding mixed fractions becomes crucial. Such connections aid in creating a cohesive learning experience that fosters curiosity and engagement.
Tips and Tricks
Making math simple is the real goal for parents and educators alike. Here’s a collection of strategies that can enhance a child's learning journey with mixed fractions:
- Incorporate visuals: Use pie charts or fraction bars to make concepts tangible.
- Relate math to daily life: Cooking measurements can provide real-life applications for mixed fractions.
- Encourage group activities: Collaborative learning can stimulate discussion and peer teaching, which enhances understanding.
Creative DIY Projects
Getting creative can make learning enjoyable and memorable. Here are some engaging DIY projects along with their benefits:
Step-by-Step Guides
Getting hands-on promotes creativity.
- Creating Fraction Cards: Kids can make cards that display mixed fractions and their improper counterparts.
- DIY Fraction Pizzas: Using paper plates, children can craft pizzas cut into fractions, visually representing mixed numbers.
Benefits of hands-on activities for children's cognitive and motor skills
Activities like crafting require fine motor skills, enhancing dexterity while also solidifying mathematical concepts through active participation.
Craft Ideas
- Fraction Wall Hangings: Make attractive wall decorations that showcase different fractions and their equivalents.
- Fraction Bingo: Create Bingo cards featuring mixed fractions that students can fill out throughout lessons.
Importance of artistic expression in children's development
Artistic activities foster not only cognitive skills but also emotional expression. Such projects allow children to articulate their understanding of mixed fractions, reinforcing their learning experience through creativity.
Understanding Mixed Fractions
When we step into the realm of mixed fractions, we're not just looking at numbers; we're unwrapping the way they function within the broader world of mathematics. Mixed fractions are essential because they blend whole numbers and fractions into a single entity. This intermingling helps students comprehend parts of a whole in a tangible, relatable manner. Moreover, understanding mixed fractions paves the way for tackling more advanced mathematical concepts down the line. If we think of it as a bridge between whole numbers and fractions, it becomes clear just how important mixed fractions are in developing more profound mathematical skills.
Definition of Mixed Fractions
A mixed fraction is a combination of a whole number and a proper fraction. For instance, in the mixed fraction 2 3/4, the '2' is the whole number, while '3/4' represents the proper fraction. This distinct setup allows for easier comprehension of quantities that exceed one whole. In various academic curricula, this understanding enables students to visualize and manipulate these values more effectively, reinforcing their mathematical literacy.
Components of Mixed Fractions
Mixed fractions consist of two major components: a whole number and a proper fraction. Both parts play significant roles in understanding the overall value of mixed fractions.
Whole Number
The whole number is the integer component in a mixed fraction. In simpler terms, it forms the backbone of the mixed fraction, indicating how many complete parts there are. Take the example of 5 1/3; the '5' signifies that there are five complete units present.
This component is advantageous because it simplifies the initial understanding of mixed fractions. It provides a straightforward entry point, allowing students to focus on the fraction aspect without being overwhelmed. However, one downside could be that some students might initially overlook the intricacies of the fraction part when they focus solely on the whole number.
Proper Fraction
On the other hand, the proper fraction indicates any portion of a whole that is less than one. In our mixed fraction example, 5 1/3, the '1/3' represents a part of something. This part highlights how whole quantities can be divided further, thus emphasizing the concept of division and fractions in a broader sense.
The beauty of a proper fraction lies in its capacity to teach students about parts, making it an indispensable tool in their mathematical arsenal. Yet, as a double-edged sword, students sometimes find it challenging to grasp how fractions can represent something smaller than a whole, especially when their focus might lean towards whole numbers.
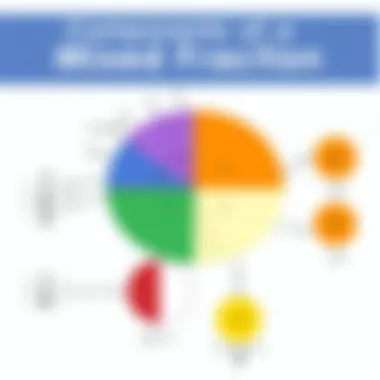
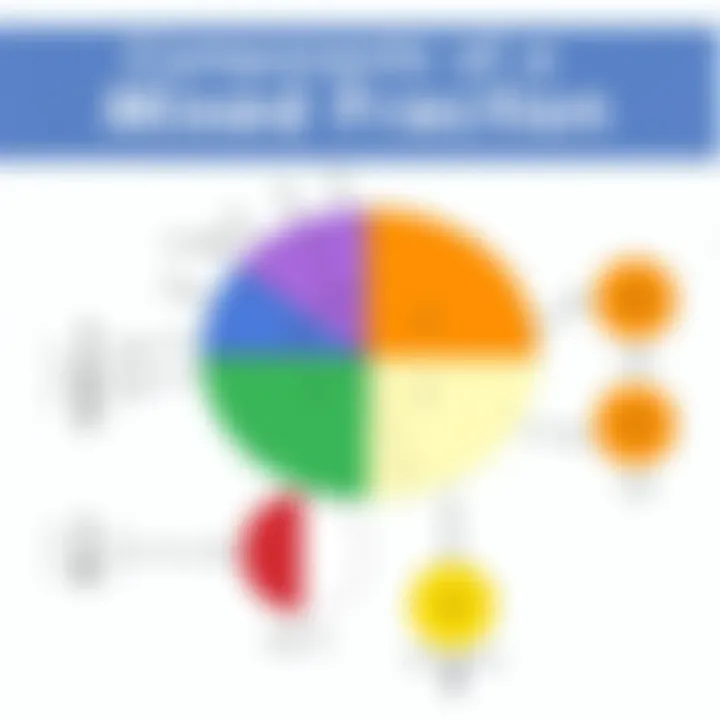
Visual Representation
Visual aids can significantly enhance a child's understanding of mixed fractions. By using pie charts or number lines, students can see how the whole number and the proper fraction come together to form one complete number. This imagery not only nurtures comprehension but also equips learners with the ability to visualize more complex fractions in various mathematical contexts.
"Visualization can often illuminate concepts that numbers alone cannot."
Why Simplify Mixed Fractions?
When grappling with mixed fractions, one might wonder why the effort to simplify them even matters. Understanding the significance of simplifying mixed fractions stands as a cornerstone for grasping various mathematical concepts. This not only enhances mathematical efficiency but also helps in establishing a clearer understanding of number relationships. Let's delve into why simplifying mixed fractions should be a priority for students, educators, and anyone who uses mathematics regularly.
Enhancing Calculation Efficiency
Understanding mixed fractions can sometimes feel like trying to find a needle in a haystack. You might have encountered a frustrating moment where a problem seemed easy, but adding or multiplying these fractions turned out to be a serious head-scratcher. Simplifying mixed fractions is like taking a shortcut in the mountains. It leads you to your destination quicker with less hassle.
In practical terms, simplifying these fractions means cutting down on computation time. For example, consider you have the mixed fraction 3 2/6. Instead of working with this value directly, converting it into a more manageable form, like 3 1/3 (after simplification), eases the math drama. This efficiency can be particularly crucial in exams or competitive scenarios where every second counts.
Understanding Mathematical Relationships
Diving into mixed fractions doesn't just help with efficiency; it also paints a clearer picture of underlying mathematical relationships. By simplifying, one draws connections between whole numbers and fractions, fostering a better grasp of how these numbers interact.
When mixed fractions are expressed in their simplest form, one can easily see how they fit into the broader mathematical framework. Consider 5 8/12. Simplifying this to 5 2/3 helps learners visualize the relationship between the whole number 5 and the fractional part 2/3, uncovering how they function together as a complete unit. This understanding becomes especially vital in more advanced topics, like algebra, where relationships between variables reign supreme.
Application in Real-World Scenarios
Mixed fractions aren't just abstract math – they frequently pop up in real life, and knowing how to simplify them can be surprisingly handy. From cooking to budgeting, these fractions can affect daily decisions. For instance, when measuring ingredients, you might encounter a recipe calling for 1 1/4 cups of flour. If you need to double the recipe, knowing how to simplify that mixed fraction into 2 1/2 cups will save time.
Moreover, in construction and carpentry, mixed fractions often arise. Measuring lengths or cuts frequently involves the use of these fractions. The ability to simplify them means that workers can work with cleaner numbers, ensuring accurate measurements and minimizing the likelihood of expensive errors.
“In the world of numbers, simplicity paves the way for clarity and precision.”
Overall, simplifying mixed fractions is not merely an academic exercise; it’s a skill with real-world relevance, impacting various aspects of life. Whether it’s speeding up math tasks, fostering a sound understanding of mathematical relationships, or making everyday scenarios easier to navigate, the benefits are clear. Recognizing the importance of simplification can empower learners to tackle mixed fractions without fear, turning a potentially complicated concept into an accessible skill.
Steps to Simplify Mixed Fractions
When it comes to simplifying mixed fractions, understanding the process is key. This section delves into the steps you need to take to handle mixed fractions efficiently. Not only does simplifying mixed fractions aid in calculations, but it also provides a clearer perspective on mathematical relationships and enhances problem-solving skills in real-world scenarios.
The process of simplification reduces mixed fractions to their most manageable forms, making them less daunting. Here’s how to tackle them, one step at a time.
Identifying the Components
Before you can simplify a mixed fraction, it's crucial to identify its core components. A mixed fraction is comprised of a whole number and a proper fraction.
For example, in the mixed fraction 2 3/4, 2 is the whole number and 3/4 is the proper fraction. Recognizing these parts gives you a starting point. This is an important step because it clarifies what you are working with and sets you up for the next phase in the simplification process.


Converting to Improper Fractions
Once you've identified the components, the next step involves converting the mixed fraction into an improper fraction. This conversion simplifies calculations and makes it easier to apply reduction techniques.
Multiplying the Whole Number
To convert a mixed fraction, you start by multiplying the whole number by the denominator of the proper fraction. Let’s take our earlier example of 2 3/4. The multiplication involves:
[ 2 \times 4 = 8 ]\
This shows you how many parts, in total, we’re dealing with.
This step is crucial because it transforms your mixed fraction into a form that's easier to manage. It's a popular choice due to its straightforwardness. When you multiply, you're effectively shifting from a composite to a simpler fraction representation. However, one might note that if the whole number is large, be careful not to miscalculate here.
Adding the Numerator
Following the multiplication, you add the numerator to the result. Continuing with the previous example:
[ 8 + 3 = 11 ]\
This means the improper fraction is 11/4. This addition is another step that simplifies your operation. It combines both parts of the fraction into one simplified figure. However, one must be attentive here as it's common for students to misinterpret what they should add, potentially confusing components.
Fraction Reduction Techniques
With an improper fraction like 11/4, you'll want to look at fraction reduction to find its simplest form.
Finding the Greatest Common Divisor
One effective way to reduce a fraction is by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both numbers evenly.
In our example, the GCD of 11 and 4 is 1, meaning this fraction is already in its simplest form. Knowing how to find the GCD can be a valuable skill, as it provides the quickest route to reducing fractions. This method is quite beneficial because it not only simplifies the process but also reinforces basic division concepts.
Simplifying the Numerator and Denominator
If the GCD was greater than 1, you would then divide both the numerator and the denominator by this number to simplify your fraction. In our case, that isn’t necessary, but it’s a vital step to remember for other fractions.
Converting Back to Mixed Fractions
The final step involves converting back to a mixed fraction if needed. If your improper fraction has a numerator greater than its denominator, like 11/4, you can find out how many whole numbers fit inside.
This tells us that 11/4 is equivalent to 2 3/4 as a mixed number again. This conversion reassures you that all your previous calculations were conducted correctly.
Each of these steps, from identifying components to converting back, is essential in simplifying mixed fractions effectively. By following this clear sequence, you’ll become proficient in dealing with these fractions, elevating your mathematical fluency to new heights.
Common Misconceptions
Understanding mixed fractions can be a bit tricky, and several misconceptions often cloud the clarity of the topic. Recognizing these misunderstandings is crucial because they can lead both students and adults down the wrong path in mathematical reasoning. The goal of this section is to clarify these points, ensuring that educators, parents, and learners are on the same page when working with mixed fractions. By addressing these misconceptions, we can promote sound mathematics education and help students develop a stronger foundation in numerical skills.
Mixing Up Mixed and Improper Fractions
A common pitfall is the confusion between mixed and improper fractions. It's easy to see why this happens. Mixed fractions, like 3 1/2, combine a whole number with a proper fraction. Meanwhile, an improper fraction, such as 7/2, contains a numerator larger than its denominator. While they're closely related, understanding their differences is vital.
This is not merely a semantic issue. The distinction impacts various operations, especially addition and subtraction. When students mistake one for the other, they may apply the wrong operational rules, leading to incorrect answers. For instance, let's say a student sees 3 1/2 and assumes it's the same as 7/2, failing to convert properly when combining with another fraction.
This confusion can lead to a lack of confidence in working with fractions in general. To combat this, educators should emphasize the definitions and properties of both forms consistently when teaching. Practical exercises that involve converting between the two types can significantly help students grasp these concepts.
Confusing Simplification and Addition/Subtraction
Another prevalent misconception involves mixing up the processes of simplification and basic operations like addition and subtraction. When tasked with simplifying a mixed fraction, some learners might try to add or subtract without first converting it to an improper fraction. For example, in an operation like 3 1/2 - 1 1/4, bypassing initial simplification could generate unnecessary complexity and lead to errors.
It's essential to note that simplification is about reducing a fraction to its simplest form. It's the process that enhances ease of understanding and calculation. In contrast, adding or subtracting requires careful alignment of fractions, necessitating a shared denominator.
Students should be encouraged to view simplification as a preparatory step toward easier operations, not an end in itself. By practicing problems that emphasize both concepts separately, learners can build confidence and skill coherently. Additionally, teachers can use visual aids to show how simplification clears the path for easier calculations, reinforcing the value of a strong foundation in mixed fractions.
Practical Exercises
When it comes to learning mixed fractions, practical exercises play a pivotal role in reinforcing concepts and enhancing understanding. Engaging in exercises allows students to practice the steps involved in simplifying mixed fractions, making the theoretical aspects more tangible. By applying the knowledge gained from previous sections, students can develop confidence in their abilities, reducing anxiety associated with math tasks. Practical exercises also illuminate common pitfalls, helping learners identify mistakes and misconceptions.
Importance of Practical Exercises:
- Reinforcement of Concepts: Revisiting the concepts through exercises solidifies understanding.
- Skill Development: Regular practice hones calculation skills essential for further mathematical studies.
- Real-world Connections: Many exercises can highlight how mixed fractions are found in everyday scenarios, making math feel applicable.
"The only way to learn mathematics is to do mathematics."
Through various examples and interactive tasks, practical exercises provide a structured way to reinforce the learning process in a gradual manner.
Examples with Step-by-Step Solutions
Providing examples with step-by-step solutions demystifies the simplification process of mixed fractions. When learners see a clear breakdown of each step, it transforms messy calculations into coherent guidelines. Let's consider an example:
Example: Simplify the mixed fraction 2 ( \frac46 ).
- Identify the components: 2 is the whole number, and ( \frac46 ) is the proper fraction.
- Convert to an improper fraction: Multiply the whole number by the denominator (2 * 6 = 12) and then add the numerator (12 + 4 = 16). The improper fraction is ( \frac166 ).
- Reduce the fraction: Find the greatest common divisor of 16 and 6, which is 2. Thus, ( \frac16 \div 26 \div 2 = \frac83 ).
- Convert back to mixed fraction: Divide the numerator by the denominator. 8 ÷ 3 = 2 remainder 2. So, the mixed fraction is 2 ( \frac23 ).
By showing each step clearly, learners can adapt these techniques to various mixed fractions, leading to a deeper understanding.
Interactive Exercises for Children
Worksheets
Worksheets serve as a fundamental tool in the learning process for children. They offer structured tasks that guide students through the simplifying of mixed fractions. A key characteristic of worksheets is their ability to present a series of problems that gradually increase in difficulty. This nurtures a sense of accomplishment as learners progress.
- Benefits: They enhance concentration and encourage independent practice, proving to be beneficial for both guided learning in classrooms and self-study at home.
- Unique Features: Worksheets can include pictorial representations or real-world scenarios that help children visualize mixed fractions, making them engaging and relatable.
While these may feel less interactive than digital tools, they encourage critical thinking and logical reasoning, cornerstones of mathematical understanding.
Online Tools
Online tools have surged in popularity, bringing a modern twist to practicing mixed fractions. These tools provide interactive platforms where students can test their knowledge through games or quizzes. A crucial characteristic is the immediate feedback they offer.
- Benefits: They often include colorful graphics and animations which keep children engaged and excited to learn. Plus, many online platforms allow for a personalized learning path, adapting to each child’s unique pace.
- Unique Features: Online tools can track a learner's progress over time. They display areas of strength and weakness, guiding parents and teachers in providing tailored support.
While the digital aspect is undeniably engaging, it’s vital to balance screen time with traditional methods to build foundational skills. The synergy between worksheets and online tools creates a comprehensive learning experience, catering to diverse learning styles.
Integrating these exercises into a regular study routine ensures that learners understand and simplify mixed fractions with ease and confidence.
Resources for Further Learning
When grappling with mixed fractions, the journey doesn’t end with mastering basic techniques; it’s just the start. Resources for further learning are essential in honing the skills necessary to navigate this complex area of mathematics. Having access to quality materials and support can help reinforce understanding and provide additional perspectives, which is particularly beneficial for children, parents, teachers, and caregivers alike. Understanding different types of educational resources can bridge gaps in knowledge and reinforce skills, ensuring that learners don’t just memorize steps but truly understand the principles behind mixed fractions.
Books and Guides
Books and guides serve as the backbone of mathematical education. They can transform abstract concepts into tangible knowledge through clear explanations and numerous examples. Look for books specifically tailored to mixed fractions that offer practice problems, visual aids, and solutions that make the learning process more interactive. Here are a few notable recommendations:
- "Math Made Easy" by Silvanus P. Thompson: This classic text breaks down complex math concepts, including mixed fractions, into bite-sized pieces.
- "The Complete Idiot's Guide to Algebra" by Amy H. Schwartz: While covering algebra broadly, it also explains fractions and mixed numbers in a way that is accessible and engaging.
- "Teaching Fractions and Ratios for Understanding" by Sandra K. Wilkins: A great resource for educators, focusing on methods to teach mixed fractions effectively.
These texts not only provide structured learning paths but also encourage critical thinking and problem-solving skills. The diversity in authors and styles allows readers to find the perfect book that aligns with their learning preferences.
Educational Websites
In today’s digital era, educational websites have become invaluable resources for learning. They offer interactive content, games, and multimedia resources that engage different learning styles. Here’s a list of effective online platforms where learners can explore mixed fractions:
- Khan Academy: This site provides video lessons and practice exercises on mixed fractions and numerous other math topics. It’s straightforward and encourages self-paced learning.
- IXL: This is an interactive learning platform focusing on various subjects, including a dedicated section for fractions. The personalized feedback can help identify areas needing improvement.
- Math is Fun: With its clear explanations and visual aids, this website demystifies mixed fractions and makes the learning process enjoyable.
Utilizing these websites can enhance understanding, as learners can practice at their own individual pace, revisit challenging concepts, and benefit from immediate feedback.
Tutoring Services
For those who prefer a more personalized approach, tutoring services can be a game-changer when learning mixed fractions. One-on-one tutoring can address specific learning needs and fill in knowledge gaps. Here are a few considerations when looking for tutoring services:
- In-Person vs. Online Tutoring: Determine what fits best; in-person sessions provide face-to-face interaction, while online tutoring offers flexibility.
- Specialization: Look for tutors who specialize in math and have a strong grasp of fractions and mixed numbers. Their expertise can significantly boost the learning curve.
- Feedback and Progress Tracking: A good tutor will regularly assess progress and adapt their teaching methods based on the learner’s needs.
Resources like Wyzant and Tutor.com are platforms where parents can find qualified math tutors ready to help their child master mixed fractions through tailored sessions.
In the quest for understanding mixed fractions, never underestimate the power of the right resources. Quality materials can turn confusion into clarity and promote a deeper appreciation for mathematics.
Closure
In wrapping up this exploration of mixed fractions, it's clear how vital it is to grasp the topic well. Simplifying mixed fractions proves not just to be an academic exercise, but also a life skill that enhances both mathematical proficiency and practical problem-solving. The whole journey through understanding, simplifying, and applying mixed fractions enriches one’s overall approach to mathematics and everyday calculations.
Summarizing Key Points
To summarize, here are the main takeaways:
- Understanding mixed fractions: Mixed fractions consist of a whole number and a proper fraction, which requires a solid grasp of basic fraction concepts.
- Importance of simplification: Simplifying mixed fractions not only makes calculations easier but also makes it simpler to comprehend mathematical relationships.
- Practical applications: From cooking to construction, understanding and simplifying mixed fractions plays a role in various real-life scenarios.
Ultimately, the knowledge gained from this guide fosters a stronger mathematical foundation. The categorization of components and the clarity on processes hold significant weight for anyone who engages with mixed fractions, whether they’re students sitting in a classroom or adults managing day-to-day tasks.
Encouraging Continual Practice
It's crucial to keep practicing mixed fractions. The journey doesn’t end with grasping the fundamentals. Regular practice solidifies concepts and enhances fluency in manipulation. Here are a few tips for continued practice:
- Interactive tools: Encourage the use of online calculators and worksheets that specialize in mixed fractions to make practice engaging. Various educational platforms have resources that can be particularly useful.
- Real-life scenarios: Look for opportunities to apply mixed fractions in daily activities. This could involve cooking recipes, portioning materials for projects, or even budgeting.
- Group activities: Learning in groups can spark lively discussions and allow learners to teach one another. This not only reinforces their understanding but also builds confidence.
With ongoing practice, these ideas about mixed fractions will transform from a challenge into a manageable skill set. Consider it as not just a topic to learn, but as a tool for enhancing critical thinking and everyday functionality. Regular engagement with mixed fractions ensures that the skills become second nature, ready for application at any time.















